배열의 크기 조정하기
일정한 크기의 배열이 주어졌을 때, 그 크기를 키우려면 어떻게 해야 할까?
단순하게 현재 배열이 저장되어 있는 메모리 위치의 바로 옆에 일정 크기의 메모리를 더 덧붙이면 되겠지만,
실제로는 다른 데이터가 저장되어 있을 확률이 높다.
따라서 안전하게 새로운 공간에 큰 크기의 메모리를 다시 할당하고 기존 배열의 값들을 하나씩 옮겨줘야 한다.
따라서 이런 작업은 O(n), 즉 배열의 크기 n만큼의 실행 시간이 소요될 것이다.
#include <stdio.h>
#include <stdlib.h>
int main(void)
{
//int 자료형 3개로 이루어진 list 라는 포인터를 선언하고 메모리 할당
int *list = malloc(3 * sizeof(int));
// 포인터가 잘 선언되었는지 확인
if (list == NULL)
{
return 1;
}
// list 배열의 각 인덱스에 값 저장
list[0] = 1;
list[1] = 2;
list[2] = 3;
//int 자료형 4개 크기의 tmp 라는 포인터를 선언하고 메모리 할당
int *tmp = malloc(4 * sizeof(int));
if (tmp == NULL)
{
return 1;
}
// list의 값을 tmp로 복사
for (int i = 0; i < 3; i++)
{
tmp[i] = list[i];
}
// tmp배열의 네 번째 값도 저장
tmp[3] = 4;
// list의 메모리를 초기화
free(list);
// list가 tmp와 같은 곳을 가리키도록 지정
list = tmp;
// 새로운 배열 list의 값 확인
for (int i = 0; i < 4; i++)
{
printf("%i\n", list[i]);
}
// list의 메모리 초기화
free(list);
}동일한 작업을 realloc 이라는 함수를 이용할 수 있다.
#include <stdio.h>
#include <stdlib.h>
int main(void)
{
int *list = malloc(3 * sizeof(int));
if (list == NULL)
{
return 1;
}
list[0] = 1;
list[1] = 2;
list[2] = 3;
// tmp 포인터에 메모리를 할당하고 list의 값 복사
int *tmp = realloc(list, 4 * sizeof(int));
if (tmp == NULL)
{
return 1;
}
// list가 tmp와 같은 곳을 가리키도록 지정
list = tmp;
// 새로운 list의 네 번째 값 저장
list[3] = 4;
// list의 값 확인
for (int i = 0; i < 4; i++)
{
printf("%i\n", list[i]);
}
//list 의 메모리 초기화
free(list);
}이미 할당된 메모리의 크기를 조절할 때 임시 메모리를 새로 할당해줘야 하는 이유는,
처음 할당된 메모리 영역 앞뒤로 이미 할당된 영역이 있을 가능성이 있으므로,
연속적인 메모리 할당을 보장할 수 없기 때문이다.
연결리스트
배열에서는 각 인덱스의 값이 메모리상에서 연이어 저장되어 있다.
하지만 꼭 그럴 필요가 있을까?
각 값이 메모리상의 여러 군데 나뉘어져 있다고 하더라도 바로 다음 값의 메모리 주소만 기억하고 있다면 여전히 값을 연이어서 읽어들일 수 있다.
이를 ‘연결 리스트’라고 한다.
아래 그림처럼 크기가 3인 연결 리스트는
각 인덱스의 메모리 주소에서 자신의 값과 함께 바로 다음 값의 주소(포인터)를 저장한다.
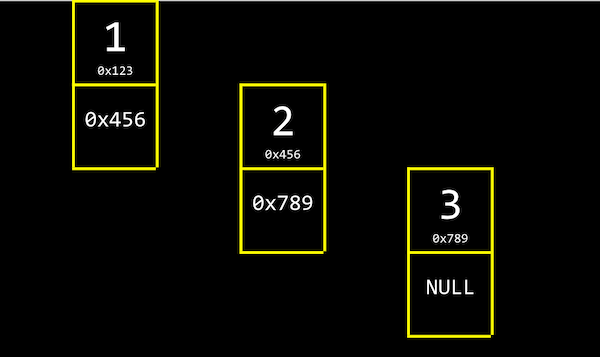
typedef struct node
{
int number;
struct node *next;
}
node;연결리스트는 위 코드처럼 간단한 구조체로 정의할 수 있다.
node 라는 이름의 구조체는 number 와 *next 두 개의 필드가 함께 정의되어 있다.
number는 각 node가 가지는 값, *next 는 다음 node를 가리키는 포인터가 된다.
여기서 typedef struct 대신에 typedef struct node 라고 ‘node’를 함께 명시해 주는 것은,
구조체 안에서 node를 사용하기 위함이다.
실제로 구현하면 아래 코드와 같다.
#include <stdio.h>
#include <stdlib.h>
//연결 리스트의 기본 단위가 되는 node 구조체를 정의한다.
typedef struct node
{
//node 안에서 정수형 값이 저장되는 변수를 name으로 지정한다.
int number;
//다음 node의 주소를 가리키는 포인터를 *next로 지정한다.
struct node *next;
}
node;
int main(void)
{
// list라는 이름의 node 포인터를 정의한다. 연결 리스트의 가장 첫 번째 node를 가리킬 것이다.
// 이 포인터는 현재 아무 것도 가리키고 있지 않기 때문에 NULL 로 초기화한다.
node *list = NULL;
// 새로운 node를 위해 메모리를 할당하고 포인터 *n으로 가리킨다.
node *n = malloc(sizeof(node));
if (n == NULL)
{
return 1;
}
// n의 number 필드에 1의 값을 저장합니다. “n->number”는 “(*n).numer”와 동일한 의미다.
// 즉, n이 가리키는 node의 number 필드를 의미하는 것이다.
// 간단하게 화살표 표시 ‘->’로 쓸 수 있습니다. n의 number의 값을 1로 저장한다.
n->number = 1;
// n 다음에 정의된 node가 없으므로 NULL로 초기화한다.
n->next = NULL;
// 이제 첫번째 node를 정의했기 떄문에 list 포인터를 n 포인터로 바꿔 준다.
list = n;
// 이제 list에 다른 node를 더 연결하기 위해 n에 새로운 메모리를 다시 할당한다.
n = malloc(sizeof(node));
if (n == NULL)
{
return 1;
}
// n의 number와 next의 값을 각각 저장한다.
n->number = 2;
n->next = NULL;
// list가 가리키는 것은 첫 번째 node이다.
//이 node의 다음 node를 n 포인터로 지정한다.
list->next = n;
// 다시 한 번 n 포인터에 새로운 메모리를 할당하고 number과 next의 값을 저장한다.
n = malloc(sizeof(node));
if (n == NULL)
{
return 1;
}
n->number = 3;
n->next = NULL;
// 현재 list는 첫번째 node를 가리키고, 이는 두번째 node와 연결되어 있다.
// 따라서 세 번째 node를 더 연결하기 위해 첫 번째 node (list)의
// 다음 node(list->next)의 다음 node(list->next->next)를 n 포인터로 지정한다.
list->next->next = n;
// 이제 list에 연결된 node를 처음부터 방문하면서 각 number 값을 출력한다.
// 마지막 node의 next에는 NULL이 저장되어 있을 것이기 때문에 이 것이 for 루프의 종료 조건이 된다.
for (node *tmp = list; tmp != NULL; tmp = tmp->next)
{
printf("%i\n", tmp->number);
}
// 메모리를 해제해주기 위해 list에 연결된 node들을 처음부터 방문하면서 free 해준다.
while (list != NULL)
{
node *tmp = list->next;
free(list);
list = tmp;
}
}
배열과 비교해서 연결 리스트는 새로운 값을 추가할 때, 다시 메모리를 할당하지 않아도 된다는 장점이 있다.
하지만 유동적인 구조는 임의 접근이 불가능하다.
예를 들어 연결리스트에 값을 추가하거나 검색하는 경우
이를 위해 해당하는 위치까지 연결 리스트의 각 노드들을 따라 이동해야 한다.
그 때 실행 시간은 O(n) 이된다.
따라서 목적에 부합하는 가장 효율적인 데이터 구조를 고민해서 사용하는 것이 중요하다.
연결리스트 (트리)
트리는 연결리스트를 기반으로 한 새로운 데이터 구조이다.
가장 높은 층에서 트리가 시작되는 노드를 ‘루트’라고 한다.
루트 노드는 다음 층의 노드들을 가리키고 있고, 이를 ‘자식 노드’라고 한다.
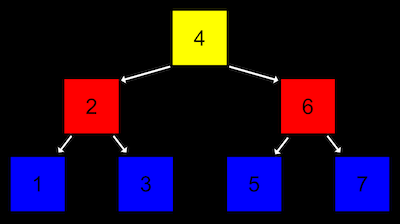
먼저 하나의 노드는 두 개의 자식 노드를 가진다.
또 왼쪽 자식 노드는 자신의 값 보다 작고, 오른쪽 자식 노드는 자신의 값보다 크다.
따라서 이런 트리 구조는 이진 검색을 수행하는데 유리하다. (이미 정렬이 되어 있고 나눠져 있기 때문)
//이진 검색 트리의 노드 구조체
typedef struct node
{
// 노드의 값
int number;
// 왼쪽 자식 노드
struct node *left;
// 오른쪽 자식 노드
struct node *right;
} node;
// 이진 검색 함수 (*tree는 이진 검색 트리를 가리키는 포인터)
bool search(node *tree)
{
// 트리가 비어있는 경우 ‘false’를 반환하고 함수 종료
if (tree == NULL)
{
return false;
}
// 현재 노드의 값이 50보다 크면 왼쪽 노드 검색
else if (50 < tree->number)
{
return search(tree->left);
}
// 현재 노드의 값이 50보다 작으면 오른쪽 노드 검색
else if (50 > tree->number)
{
return search(tree->right);
}
// 위 모든 조건이 만족하지 않으면 노드의 값이 50이므로 ‘true’ 반환
else {
return true;
}
}이진 검색 트리를 활용하였을 때 검색 실행 시간과 노드 삽입 시간은 모두 O(log n) 이다.
해시테이블
연결 리스트의 배열이다.
각 값들은 해시함수라는 맞춤형 함수를 통해서 어떤 바구니에 담기는 지가 결정된다.
예를 든 그림을 보면
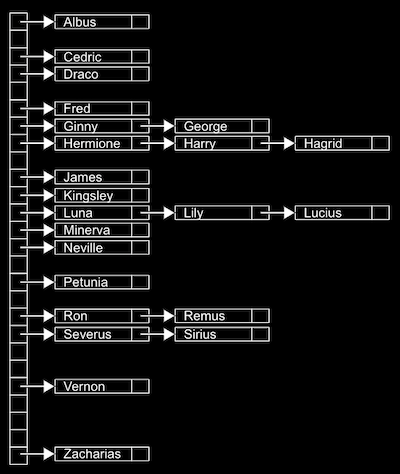
사람의 이름이 해시 테이블에 저장되며,
‘이름의 가장 첫 글자’인 경우를 생각해 보겠다.
그 경우 알파벳 개수에 해당하는 총 26개의 포인터들이 있을 수 있으며,
각 포인터는 그 알파벳을 시작으로 하는 이름들을 저장하는 연결 리스트를 가리키게 된다.
만약 해시 함수가 이상적이라면, 각 바구니에는 단 하나의 값들만 담기게 될 것이다.
따라서 검색 시간은 O(1)이 된다.
하지만 그렇지 않은 경우, 최악의 상황에는 단 하나의 바구니에 모든 값들이 담겨서 O(n)이 될 수도 있다.
일반적으로는 최대한 많은 바구니를 만드는 해시 함수를 사용하기 때문에 거의 O(1)에 가깝다고 볼 수 있다.
트라이
트라이는 기본적으로 ‘트리’ 형태의 자료 구조이다.
각 노드가 ‘배열’로 이루어져있다는 것이다.
아래 그림과 같이 Hermione, Harry, Hagrid 세 문자열을 트라이에 저장해보겠다.
루트 노드를 시작으로 각 화살표가 가리키는 알파벳을 따라가면서 노드를 이어주면 된다.
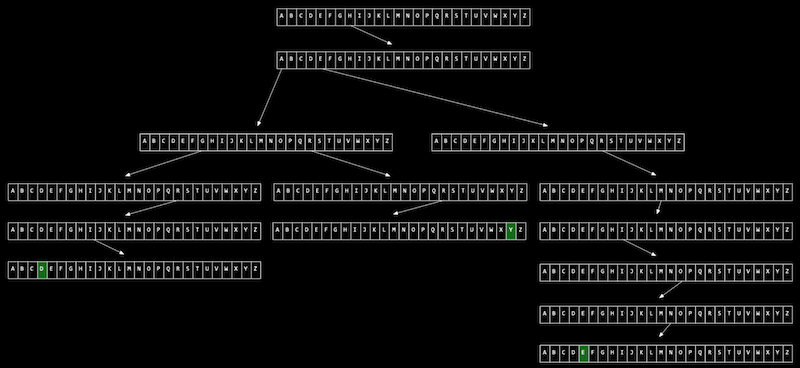
위와 같은 트라이에서 값을 검색하는데 걸리는 시간은 ‘문자열의 길이’에 의해 한정된다.
단순히 문자열의 각 문자를 보며 트리를 탐색해나가기만 하면 되기 때문이다.
일반적인 영어 이름의 길이를 n이라고 했을 때, 검색 시간은 O(n)이 되지만,
대부분의 이름은 그리 크지 않은 상수값(예, 20자 이내)이기 때문에 O(1)이나 마찬가지라고 볼 수 있다.
하지만 역시 단점이 있는데 각 배열에을 저장하다 보니 경우의 수가 26^n 꼴로 증가하게 되서 메모리에 대한 생각을 해야 한다.
스택, 큐, 딕셔너리
스택
메모리 구조에서 살펴봤듯이 값이 위로 쌓이는 구조이다.
따라서 값을 넣고 뺄 때 ‘후입 선출’ 또는 ‘LIFO’라는 방식을 따르게 된다.
즉, 가장 나중에 들어온 값이 가장 먼저 나간다.
뷔페에서 접시를 쌓아 뒀을 때 사람들이 가장 위에 있는(즉, 가장 나중에 쌓인) 접시를 가장 먼저 들고 가는 것과 동일하다.
배열이나 연결 리스트를 통해 구현 가능하다.
큐
값이 위로 쌓이는 구조이다.
따라서 값을 넣고 뺄 때 ‘후입 선출’ 또는 ‘LIFO’라는 방식을 따르게 된다.
가장 나중에 들어온 값이 가장 먼저 나간다.
뷔페에서 접시를 쌓아 뒀을 때 사람들이 가장 위에 있는(즉, 가장 나중에 쌓인) 접시를 가장 먼저 들고 가는 것과 동일하다.
배열이나 연결 리스트를 통해 구현 가능하다.
딕셔너리
‘키’와 ‘값’이라는 요소로 이루어져 있다.
‘키’에 해당하는 ‘값’을 저장하고 읽어온다.
마치 대학교에서 ‘학번’에 따라서 ‘학생’이 결정되는 것과 동일하다.
일반적인 의미에서 ‘해시 테이블’과 동일한 개념이라고도 볼 수 있다.
‘키’를 어떻게 정의할 것인지가 중요하다.
'🖥️Computer Science > CS50' 카테고리의 다른 글
| CS50_메모리 (0) | 2023.06.13 |
|---|---|
| CS50_알고리즘 (0) | 2023.06.13 |
| CS50_배열 (0) | 2023.06.13 |
| CS50_C언어 (0) | 2023.06.06 |
| CS50_컴퓨팅 사고 (0) | 2023.06.06 |
배열의 크기 조정하기
일정한 크기의 배열이 주어졌을 때, 그 크기를 키우려면 어떻게 해야 할까?
단순하게 현재 배열이 저장되어 있는 메모리 위치의 바로 옆에 일정 크기의 메모리를 더 덧붙이면 되겠지만,
실제로는 다른 데이터가 저장되어 있을 확률이 높다.
따라서 안전하게 새로운 공간에 큰 크기의 메모리를 다시 할당하고 기존 배열의 값들을 하나씩 옮겨줘야 한다.
따라서 이런 작업은 O(n), 즉 배열의 크기 n만큼의 실행 시간이 소요될 것이다.
#include <stdio.h>
#include <stdlib.h>
int main(void)
{
//int 자료형 3개로 이루어진 list 라는 포인터를 선언하고 메모리 할당
int *list = malloc(3 * sizeof(int));
// 포인터가 잘 선언되었는지 확인
if (list == NULL)
{
return 1;
}
// list 배열의 각 인덱스에 값 저장
list[0] = 1;
list[1] = 2;
list[2] = 3;
//int 자료형 4개 크기의 tmp 라는 포인터를 선언하고 메모리 할당
int *tmp = malloc(4 * sizeof(int));
if (tmp == NULL)
{
return 1;
}
// list의 값을 tmp로 복사
for (int i = 0; i < 3; i++)
{
tmp[i] = list[i];
}
// tmp배열의 네 번째 값도 저장
tmp[3] = 4;
// list의 메모리를 초기화
free(list);
// list가 tmp와 같은 곳을 가리키도록 지정
list = tmp;
// 새로운 배열 list의 값 확인
for (int i = 0; i < 4; i++)
{
printf("%i\n", list[i]);
}
// list의 메모리 초기화
free(list);
}동일한 작업을 realloc 이라는 함수를 이용할 수 있다.
#include <stdio.h>
#include <stdlib.h>
int main(void)
{
int *list = malloc(3 * sizeof(int));
if (list == NULL)
{
return 1;
}
list[0] = 1;
list[1] = 2;
list[2] = 3;
// tmp 포인터에 메모리를 할당하고 list의 값 복사
int *tmp = realloc(list, 4 * sizeof(int));
if (tmp == NULL)
{
return 1;
}
// list가 tmp와 같은 곳을 가리키도록 지정
list = tmp;
// 새로운 list의 네 번째 값 저장
list[3] = 4;
// list의 값 확인
for (int i = 0; i < 4; i++)
{
printf("%i\n", list[i]);
}
//list 의 메모리 초기화
free(list);
}이미 할당된 메모리의 크기를 조절할 때 임시 메모리를 새로 할당해줘야 하는 이유는,
처음 할당된 메모리 영역 앞뒤로 이미 할당된 영역이 있을 가능성이 있으므로,
연속적인 메모리 할당을 보장할 수 없기 때문이다.
연결리스트
배열에서는 각 인덱스의 값이 메모리상에서 연이어 저장되어 있다.
하지만 꼭 그럴 필요가 있을까?
각 값이 메모리상의 여러 군데 나뉘어져 있다고 하더라도 바로 다음 값의 메모리 주소만 기억하고 있다면 여전히 값을 연이어서 읽어들일 수 있다.
이를 ‘연결 리스트’라고 한다.
아래 그림처럼 크기가 3인 연결 리스트는
각 인덱스의 메모리 주소에서 자신의 값과 함께 바로 다음 값의 주소(포인터)를 저장한다.

typedef struct node
{
int number;
struct node *next;
}
node;연결리스트는 위 코드처럼 간단한 구조체로 정의할 수 있다.
node 라는 이름의 구조체는 number 와 *next 두 개의 필드가 함께 정의되어 있다.
number는 각 node가 가지는 값, *next 는 다음 node를 가리키는 포인터가 된다.
여기서 typedef struct 대신에 typedef struct node 라고 ‘node’를 함께 명시해 주는 것은,
구조체 안에서 node를 사용하기 위함이다.
실제로 구현하면 아래 코드와 같다.
#include <stdio.h>
#include <stdlib.h>
//연결 리스트의 기본 단위가 되는 node 구조체를 정의한다.
typedef struct node
{
//node 안에서 정수형 값이 저장되는 변수를 name으로 지정한다.
int number;
//다음 node의 주소를 가리키는 포인터를 *next로 지정한다.
struct node *next;
}
node;
int main(void)
{
// list라는 이름의 node 포인터를 정의한다. 연결 리스트의 가장 첫 번째 node를 가리킬 것이다.
// 이 포인터는 현재 아무 것도 가리키고 있지 않기 때문에 NULL 로 초기화한다.
node *list = NULL;
// 새로운 node를 위해 메모리를 할당하고 포인터 *n으로 가리킨다.
node *n = malloc(sizeof(node));
if (n == NULL)
{
return 1;
}
// n의 number 필드에 1의 값을 저장합니다. “n->number”는 “(*n).numer”와 동일한 의미다.
// 즉, n이 가리키는 node의 number 필드를 의미하는 것이다.
// 간단하게 화살표 표시 ‘->’로 쓸 수 있습니다. n의 number의 값을 1로 저장한다.
n->number = 1;
// n 다음에 정의된 node가 없으므로 NULL로 초기화한다.
n->next = NULL;
// 이제 첫번째 node를 정의했기 떄문에 list 포인터를 n 포인터로 바꿔 준다.
list = n;
// 이제 list에 다른 node를 더 연결하기 위해 n에 새로운 메모리를 다시 할당한다.
n = malloc(sizeof(node));
if (n == NULL)
{
return 1;
}
// n의 number와 next의 값을 각각 저장한다.
n->number = 2;
n->next = NULL;
// list가 가리키는 것은 첫 번째 node이다.
//이 node의 다음 node를 n 포인터로 지정한다.
list->next = n;
// 다시 한 번 n 포인터에 새로운 메모리를 할당하고 number과 next의 값을 저장한다.
n = malloc(sizeof(node));
if (n == NULL)
{
return 1;
}
n->number = 3;
n->next = NULL;
// 현재 list는 첫번째 node를 가리키고, 이는 두번째 node와 연결되어 있다.
// 따라서 세 번째 node를 더 연결하기 위해 첫 번째 node (list)의
// 다음 node(list->next)의 다음 node(list->next->next)를 n 포인터로 지정한다.
list->next->next = n;
// 이제 list에 연결된 node를 처음부터 방문하면서 각 number 값을 출력한다.
// 마지막 node의 next에는 NULL이 저장되어 있을 것이기 때문에 이 것이 for 루프의 종료 조건이 된다.
for (node *tmp = list; tmp != NULL; tmp = tmp->next)
{
printf("%i\n", tmp->number);
}
// 메모리를 해제해주기 위해 list에 연결된 node들을 처음부터 방문하면서 free 해준다.
while (list != NULL)
{
node *tmp = list->next;
free(list);
list = tmp;
}
}
배열과 비교해서 연결 리스트는 새로운 값을 추가할 때, 다시 메모리를 할당하지 않아도 된다는 장점이 있다.
하지만 유동적인 구조는 임의 접근이 불가능하다.
예를 들어 연결리스트에 값을 추가하거나 검색하는 경우
이를 위해 해당하는 위치까지 연결 리스트의 각 노드들을 따라 이동해야 한다.
그 때 실행 시간은 O(n) 이된다.
따라서 목적에 부합하는 가장 효율적인 데이터 구조를 고민해서 사용하는 것이 중요하다.
연결리스트 (트리)
트리는 연결리스트를 기반으로 한 새로운 데이터 구조이다.
가장 높은 층에서 트리가 시작되는 노드를 ‘루트’라고 한다.
루트 노드는 다음 층의 노드들을 가리키고 있고, 이를 ‘자식 노드’라고 한다.

먼저 하나의 노드는 두 개의 자식 노드를 가진다.
또 왼쪽 자식 노드는 자신의 값 보다 작고, 오른쪽 자식 노드는 자신의 값보다 크다.
따라서 이런 트리 구조는 이진 검색을 수행하는데 유리하다. (이미 정렬이 되어 있고 나눠져 있기 때문)
//이진 검색 트리의 노드 구조체
typedef struct node
{
// 노드의 값
int number;
// 왼쪽 자식 노드
struct node *left;
// 오른쪽 자식 노드
struct node *right;
} node;
// 이진 검색 함수 (*tree는 이진 검색 트리를 가리키는 포인터)
bool search(node *tree)
{
// 트리가 비어있는 경우 ‘false’를 반환하고 함수 종료
if (tree == NULL)
{
return false;
}
// 현재 노드의 값이 50보다 크면 왼쪽 노드 검색
else if (50 < tree->number)
{
return search(tree->left);
}
// 현재 노드의 값이 50보다 작으면 오른쪽 노드 검색
else if (50 > tree->number)
{
return search(tree->right);
}
// 위 모든 조건이 만족하지 않으면 노드의 값이 50이므로 ‘true’ 반환
else {
return true;
}
}이진 검색 트리를 활용하였을 때 검색 실행 시간과 노드 삽입 시간은 모두 O(log n) 이다.
해시테이블
연결 리스트의 배열이다.
각 값들은 해시함수라는 맞춤형 함수를 통해서 어떤 바구니에 담기는 지가 결정된다.
예를 든 그림을 보면

사람의 이름이 해시 테이블에 저장되며,
‘이름의 가장 첫 글자’인 경우를 생각해 보겠다.
그 경우 알파벳 개수에 해당하는 총 26개의 포인터들이 있을 수 있으며,
각 포인터는 그 알파벳을 시작으로 하는 이름들을 저장하는 연결 리스트를 가리키게 된다.
만약 해시 함수가 이상적이라면, 각 바구니에는 단 하나의 값들만 담기게 될 것이다.
따라서 검색 시간은 O(1)이 된다.
하지만 그렇지 않은 경우, 최악의 상황에는 단 하나의 바구니에 모든 값들이 담겨서 O(n)이 될 수도 있다.
일반적으로는 최대한 많은 바구니를 만드는 해시 함수를 사용하기 때문에 거의 O(1)에 가깝다고 볼 수 있다.
트라이
트라이는 기본적으로 ‘트리’ 형태의 자료 구조이다.
각 노드가 ‘배열’로 이루어져있다는 것이다.
아래 그림과 같이 Hermione, Harry, Hagrid 세 문자열을 트라이에 저장해보겠다.
루트 노드를 시작으로 각 화살표가 가리키는 알파벳을 따라가면서 노드를 이어주면 된다.

위와 같은 트라이에서 값을 검색하는데 걸리는 시간은 ‘문자열의 길이’에 의해 한정된다.
단순히 문자열의 각 문자를 보며 트리를 탐색해나가기만 하면 되기 때문이다.
일반적인 영어 이름의 길이를 n이라고 했을 때, 검색 시간은 O(n)이 되지만,
대부분의 이름은 그리 크지 않은 상수값(예, 20자 이내)이기 때문에 O(1)이나 마찬가지라고 볼 수 있다.
하지만 역시 단점이 있는데 각 배열에을 저장하다 보니 경우의 수가 26^n 꼴로 증가하게 되서 메모리에 대한 생각을 해야 한다.
스택, 큐, 딕셔너리
스택
메모리 구조에서 살펴봤듯이 값이 위로 쌓이는 구조이다.
따라서 값을 넣고 뺄 때 ‘후입 선출’ 또는 ‘LIFO’라는 방식을 따르게 된다.
즉, 가장 나중에 들어온 값이 가장 먼저 나간다.
뷔페에서 접시를 쌓아 뒀을 때 사람들이 가장 위에 있는(즉, 가장 나중에 쌓인) 접시를 가장 먼저 들고 가는 것과 동일하다.
배열이나 연결 리스트를 통해 구현 가능하다.
큐
값이 위로 쌓이는 구조이다.
따라서 값을 넣고 뺄 때 ‘후입 선출’ 또는 ‘LIFO’라는 방식을 따르게 된다.
가장 나중에 들어온 값이 가장 먼저 나간다.
뷔페에서 접시를 쌓아 뒀을 때 사람들이 가장 위에 있는(즉, 가장 나중에 쌓인) 접시를 가장 먼저 들고 가는 것과 동일하다.
배열이나 연결 리스트를 통해 구현 가능하다.
딕셔너리
‘키’와 ‘값’이라는 요소로 이루어져 있다.
‘키’에 해당하는 ‘값’을 저장하고 읽어온다.
마치 대학교에서 ‘학번’에 따라서 ‘학생’이 결정되는 것과 동일하다.
일반적인 의미에서 ‘해시 테이블’과 동일한 개념이라고도 볼 수 있다.
‘키’를 어떻게 정의할 것인지가 중요하다.
'🖥️Computer Science > CS50' 카테고리의 다른 글
| CS50_메모리 (0) | 2023.06.13 |
|---|---|
| CS50_알고리즘 (0) | 2023.06.13 |
| CS50_배열 (0) | 2023.06.13 |
| CS50_C언어 (0) | 2023.06.06 |
| CS50_컴퓨팅 사고 (0) | 2023.06.06 |
